Modules
Modules occur in documents level, contain declarations and have an associated MMT URI of the form <NAMESPACE>?<NAME>, with the namespace of the current document. Modules are delimited with the symbol 
Theories
Theories are simply named groups of declarations. Examples for theories are first-order or higher-order theories, logics, type theories, logical frameworks. Their conrete syntax is
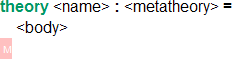
where <body> is a sequence of declarations. The context available to any specific declaration is everything provided by previous declarations, specifically theory inclusions and everything provided by the meta theory.
The meta theory statement is optional and behaves like a theory inclusion.
Theories can be nested, like this:

in which case the visible context of both the inner theory as well as <laterbody> is <previousbody>, i.e. the inner theory can see all previous declarations of the outer theory, but at no point can the outer theory see inside the inner theory (unless explicitely included).
Views
Given two theories A and B, a view from A to B maps all declarations in A to expressions over symbols in B, while preserving typing judgments. i.e. if |- a : tpA in A and v:A->B is a view, then |- v(a) : v(tpA). Hence, views are truth preserving. A is the domain of v and B is the codomain.
Their conrete syntax is

where <assignments> is a list of assignment declarations. Their syntax looks like this:
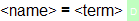
In assignments, <name> has to be a symbol declared in (the dependency closure of) <domain>, whereas <term> has to be a well-formed term over symbols in <codomain> preserving typing judgments.
Metadata
Modules can have arbitrary metadata, similar to how declarations can have arbitrary metadata associated to them:
theory MyTheory =
myAnnotationKey ❙
myAnnotationKey2 ❙
myAnnotationValue ❙
myAnnotationValue2❙
meta ?myAnnotationKey ?myAnnotationValue ❙
meta ?myAnnotationKey2 ?myAnnotationValue2❙
❚
// Also possible in views: ❚
view v : ?MyTheory -> ... =
// Do the symbols come from the domain theory? ❙
meta ?myAnnotationKey ?myAnnotationValue ❙
meta ?myAnnotationKey2 ?myAnnotationValue2❙
❚
See the corresponding section on metadata for declarations on how each meta line is structured. Note that you can have multiple metadatums on the same theory with the same key. In the implementation the metadatums form a list, hence this is allowed.
Morphisms
The semantics of the large scale structure of developments in MMT is computed in the category of theories and theory morphisms.
Atomic morphisms can be declared in two ways: via views and structures. Complex morphisms can be built in particular using composition.
Implicit Morphisms
Every development in MMT yields a specific category of theories and morphisms.
Among those, MMT distinguishes the implicit morphisms.
For any two theories A and B, there may be at most one implicit morphism from A to B.
The implicit morphisms are the following:
- any view or structure preceded by the keyword
implicit - all includes
- the identity morphism of all theories
- all compositions of implciit morphisms
Thus, technically the implicit morphisms form a thin broad subcategory of the category of theories and morphisms.
The semantics of an implicit morphism m from A to B is that every declaration of A is also visible to B, i.e., any well-formed term t over A is also well-formed over B.
The meaning of t in B is m(t).
Examples
- The intended semantics of includes is induced by the above: an include from
AtoBis an implicit morphism, which maps every term to itself. Thus, the effect of an include fromAtoBis that every term ofAcan be used inBwith the same meaning. - Consider a user who would like to add a defined declaration
c:a=tto a theoryTthat she does not have write access to. She could declare a theoryT2that includesT. But then the new declaration would only be available in theories that useT2. Instead, she would like to extendTitself from the outside, i.e., without changing it. She can achieve that by declaring a theoryT2that containsc:aand an implicit view fromT2toTthat mapsc=t. Then she can useT2?cwhereverTis used. - Realms were introduced as a language feature for providing a single interface to a large set of theories. Realms can be realized in MMT by simply making all involved morphisms implicit.