MMT - Diagrams & Diagram Operators

Diagrams & Diagram Operators

Large archives of formalizations in MMT span big theory graphs comprised of many theories and views. Often, certain subgraphs form a semantically coherent entity, a diagram.

Diagram operators are meta-programming facilities which accept diagrams of formalization as input and output new diagrams. As such, they help making large archives of formalization less redundant and more concise.

As of December 2020, MMT has preliminary support for diagram operators following an accepted paper on Structure-Preserving Diagram Operators.

Operators in MMT are Scala classes that can be bound to MMT symbols and hence accessed from MMT surface syntax.

Usage

todo: elaborate more

theory TestDiagram =
  include ur:?DiagramOperators ❙
  diag = RAWDIAG ?A ?B ?C ?v ❙
❚
diagram diagramName : ?metaTheory := DIAGOP ?TestDiagram?diag ❚

Caste Study: Universal Algebra

Consider formalizing the algebraic hierarchy with theories for magmas, monoids, groups, and more. Creating the theories for homomorphisms of magmas, monoids, and groups, respectively would not only be cumbersome to do manually, but also redundant, as according to universal algebra, there is a systematic way to derive the theories of homomorphisms given the underlying algebraic theories. Leveraging a diagram operator to generate the theories of homomorphisms also has the advantage that whenever anything changes in the algebraic theories, all homomorphism theories can be re-generated by simply rebuilding the MMT archive.

Similar automatic derivations are possible for the theories of substructures and congruences of magmas, semigroups, and so on. The following diagram pictures all theories and views that can be generated from a single SFOL theory X by means of the diagram operators implemented so far (2020-12-16):

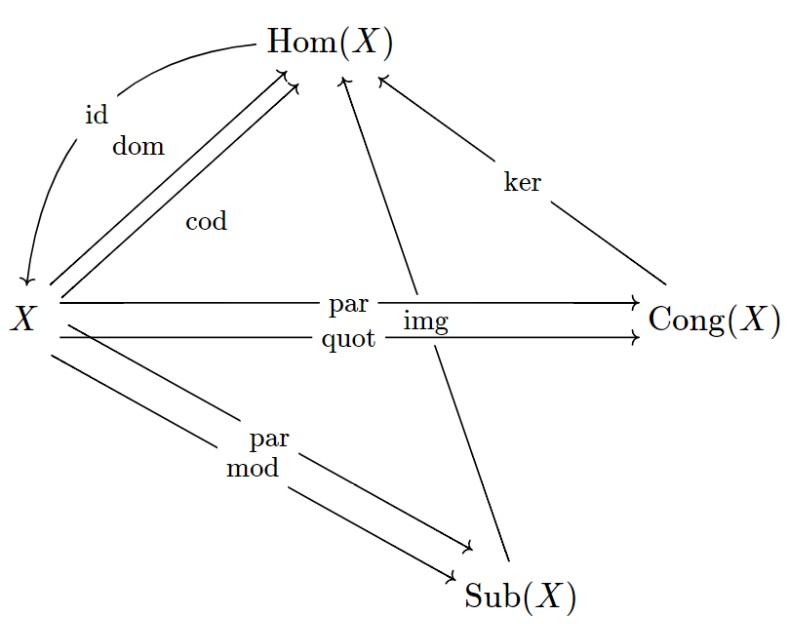
Universal algebra diagram operators Hom, Sub, Cong, and connectors

Refactoring via Diagram Operators

Theory Intersections

Imagine MMT theories Nat and Strings for natural numbers and strings. Do they share redundant parts? In some sense, they do since natural numbers form a monoid (wrt. multiplication) and strings do, too (wrt. concatenation). Suppose we realized that both theories share a redundant part by having found a partial view Nat -> Strings. With that, we can reorganize the original theories by means of performing a theory intersection (see paper, MSc. thesis).

The ability to compute theory intersections is exposed as diagram operators, too.

Example input:

theory Nat =
  N: type ❙
  zero: N ❙
  succ: N ⟶ N ❙
  plus: N ⟶ N ⟶ N ❙
  mult: N ⟶ N ⟶ N ❙
❚

theory Strings =
  str: type ❙
  empty: str ❙
  concat: str ⟶ str ⟶ str ❙
  eol_string: str ❙
❚

view PosPlusToStrings : ?Nat -> ?Strings =
  N = str ❙
  zero = empty ❙
  plus = concat ❙
❚

Diagram operator invocation: diagram IntersecterTestDiagram : ur:?RefactoringOperators := BINARY_INTERSECT ?PosPlusToStrings ❚

Output:

theory NatR : ur:?LF  = 
	include ☞ur:/modexp-test?NatIntersectsStrings ❙
	succ	
		: N⟶N
	❙
	mult	
		: N⟶N⟶N
	❙
❚

theory NatIntersectsStrings : ur:?LF  = 
	N	
		: type
	❙
	zero	
		: N
	❙
	plus	
		: N⟶N⟶N
	❙
❚

theory StringsIntersectsNat : ur:?LF  = 
	str	
		: type
	❙
	empty	
		: str
	❙
	concat	
		: str⟶str⟶str
	❙
❚

theory StringsR : ur:?LF  = 
	include ☞ur:/modexp-test?StringsIntersectsNat ❙
	eol_string	
		: str
	❙
❚

view NatIntersectsStringstoStringsIntersectsNat : ur:/modexp-test?NatIntersectsStrings  -> ur:/modexp-test?StringsIntersectsNat  = 
	N	
		= str
	❙
	zero	
		= empty
	❙
	plus	
		= concat
	❙
❚

view StringsIntersectsNattoNatIntersectsStrings : ur:/modexp-test?StringsIntersectsNat  -> ur:/modexp-test?NatIntersectsStrings  = 
	str	
		= N
	❙
	empty	
		= zero
	❙
	concat	
		= plus
	❙
❚