Content Elements
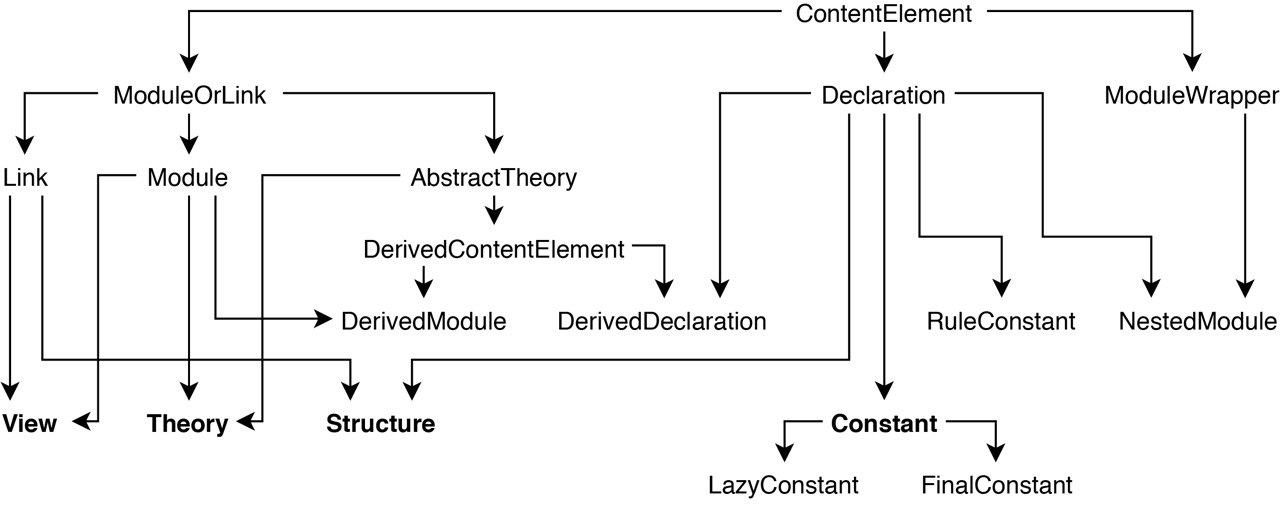
api.ContentElement can be roughly separated into two categories - declarations (constants and structures - includes are a special case of structures) and modules (theories and views). Both declarations can be links between two theories (structures and views) and can be a ContainerElement containing declarations (declared theories, structures and views). It provides the foreachDeclaration method that takes a function argument and applies it to all content elements recursively contained within it (including itself). The path method returns a ContentPath.
General
modules.ModuleOrLinkis the trait governing all content elements that contain declarations (such as theories, views, structures). It provides the following useful methods:addadds a new Declaration to the body.gettakes a LocalName and returns the declaration of that name. If no declaration by that name exists, it throws an error. The methodgetOdoes not, but returns anOption[Declaration]instead.declarestakes aLocalNameand returns aboolindicating, whether a declaration by that name exists in the body.deletetakes aLocalNameand deletes the declaration by that name from the body.updatetakes aDeclarationand adds it to the body, if no declaration by that name already exists, or replaces the existing one otherwise.getDeclarationsreturns aList[Declaration]of all declarations in the body. All final extensions ofModuleOrLinkcan be declared or defined. Declared Modules/Links have no definiens and contain primitive declarations. Defined Modules/Links have a definiens (e.g. a theory expression) that can be elaborated into a list of declarations. In either case, the (primitive or elaborated) declarations are accessed via the above methods.
modules.Linkis the trait for theory morphisms like views and structures. It has the methodsfromandto(returningTerm) for domain and codomain,codomainAsContextandtoTerm.
Modules
modules.Moduleis the top level data structure for theories and views. Thepathmethod returnsMPath.DeclaredModuleextendsModulewith aBody.-
modules.Theoryis the data structure representing theories. The class constructor takes as arguments the document/namespace containing the theory (DPath), its name (LocalName) and an optional meta theory (Option[MPath]).Theoryprovides the following useful methods:getConstantsyields those declarations in the body, that are constants (asList[Constant]).getIncludesyields aList[MPath]of the included theories, including the meta theory.getIncludesWithoutMetadoes the same without the meta theory.getNamedStructuresyields aList[Structure]of those structures that are not plain includes.
modules.Viewsimply combinesLinkandModule.
Declarations
symbols.Declarationrepresents everything on the declaration level - this entails constants, structures, derived declarations and nested modules. Thehomemethod returns the containing module (asTerm). Thepathmethod returnsGlobalName.-
symbols.Constantrepresents a constant declaration. Constants are ultimately instantiated with the subclassFinalConstant. Constants useTermContainers to store their type and definiens (in their different statesread,parsedandanalyzed), which can be accessed by the methodstpC(for types) anddfC(for definitions). The methodstpanddfcircumvent the containers and directly yield their (ideally fully analyzed) type or definiens asOption[Term].The helper object
symbols.Constanthas an apply method to conveniently create new instances ofFinalConstant. It takes as arguments the containing home module (Term), the name of the constant (LocalName), and optionally aliases (List[LocalName]), type (Option[Term]), definition (Option[Term]), role (Option[String]) and notation (NotationContainer, by default a new empty one). -
symbols.StructurecombinesLinkwithDeclaration. It has abooleanvalueisIncludesignifying whether the structure is a simple theory include.The helper objects
symbols.Structureandsymbols.SimpleStructureadd convenient apply/unapply methods, whereSimpleindicates the case where the domain is anMPath(as opposed to a complex term representing a theory expression). The helper objectssymbols.Includeandsymbols.PlainIncludeoffer apply/unapply methods for theory inclusions.