2 - A First Theory
We can now open the fol.mmt file in source with jEdit. If you haven’t done so already, I recommend you read the sections on delimiters, theories and constants now, so you know how to produce our following basic theory:
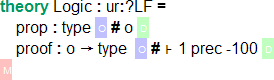
(if abbreviations are activated in jEdit, the → symbol can be produced with the abbreviation jra and the ⊦ symbol with jvdash)
This code first introduces a new theory named Logic - delimited by  - with meta theory
- with meta theory ur:?LF. The abbrivation ur expands to the URI http://cds.omdoc.org/urtheories/ - the namespace of the urtheories archive, which contains the theory LF. The fully qualified URI is thus http://cds.omdoc.org/urtheories?LF (which we could have written instead). We will go into the details of LF later.
The full URI of our new theory is made up of its name (Logic) and the namespace declared in the MANIFEST.MF file, i.e. http://kwarc.github.io/MMT?Logic.
This theory contains two constants:
propwith typetype.typeis provided by LF and is a universe, which means every symbol with typetypeis inhabitable (i.e. may occur to the right side of a typing judgment).propwill be the type of our propositions. We give it an optional notationofor brevity.proofwith typeo → typeand notation⊦ 1.→is the simple function type constructor and again provided by LF.ois just a notation forprop, soproofis a function that maps propositions to types (more on that later). We give the notation a very low precedence.
We can now parse the document and have MMT type check it. If parse-on-key is not activated (see here), you can press the parse button (arrow symbol to the top left of the screenshot below) in SideKick, after which it will show the document tree:
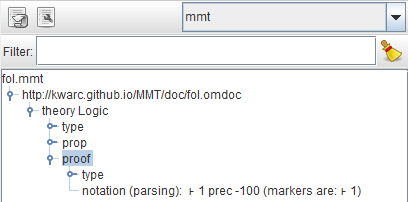
Unlike SideKick, the ErrorList window should show nothing - meaning the document type checks correctly. Let’s see what happens, if we introduce a simple typo in the type of proof, by changing it to o → tupe. This is what the ErrorList should show now:
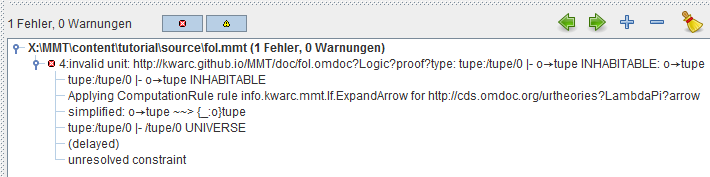
We will look at the details of the error message, after we’ve looked at LF and its rules. For now, we will remove the typo and continue with a theory specifying the syntax of propositional logic. On the basis of the theory we already have, what’s missing are the usual logical connectives ∧ (jwedge), ∨ (jvee), ⇒ (jrA), ¬ (jneg) and ⇔ (jLeftrightarrow), and constants ⊤ (jtop) and ⊥ (jbot).
For the sake of modularity, we will put those in a new theory, like so:

So we specify the connectives as functions between propositions - e.g. and takes two propositions (of type o=prop) and returns a new proposition. We assign precedences according to standard mathematical convention - e.g. ∧ binds stronger than e.g. ⇒. Constants don’t need a precedence. The include-statement makes sure, that the previously declared symbol o is available in this new theory.
We can test this, by looking at the syntax tree in SideKick. Let’s add a new constant to our theory:
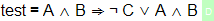
After pressing the parse-button, SideKick should show the following tree:
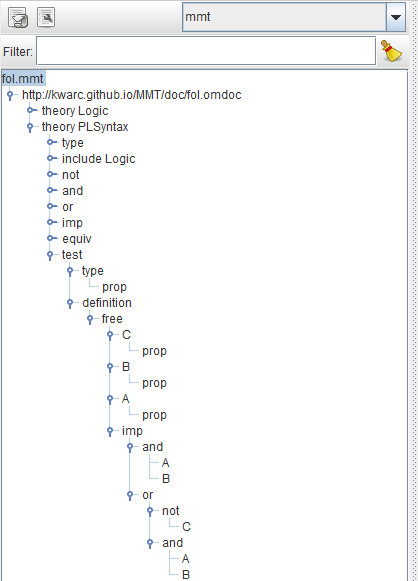
This tells us:
- MMT has correctly inferred the type of
testasprop, - MMT does not know the symbols
A,BandC, so it considers them free variables and (correctly) infers their types asprop, - MMT parses the term correctly as
(A ∧ B) ⇒ ((¬ C) ∨ (A ∧ B)).
It should be noted, that notations are always optional - we neither have to provide notations for new constants, nor do we have to use them after declaring them. We can always just use the name of the constant itself as a notation. The test constant above could have just as well been declared as:
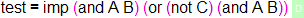
You can check the syntax trees for both variants in SideKick and verify, that they indeed match.